Ứng dụng lý thuyết IRT trong việc đánh giá đề thi và năng lực học sinh
Edmicro Ltd.
Trong việc thống kê, phân tích đề thi và năng lực học sinh trong các kỳ thi tập trung, một trong những phương pháp được sử dụng khá hiệu quả tại nhiều quốc gia trên thế giới là lý thuyết “đáp ứng câu hỏi” (IRT). Tại Mỹ, IRT được ứng dụng trong kỳ thi đầu vào xét tuyển bậc thạc sỹ kỹ thuật (GRE) và kinh tế (GMAT) [1]. Mặc dù được nghiên cứu và phát triển từ rất sớm, từ những năm 50 của thế kỷ trước, nhưng IRT vẫn chứng minh được tính hiệu quả của mình.
Trước đây, theo phương pháp đánh giá truyền thống, năng lực thí sinh chỉ được đánh giá dựa vào mức độ hoàn thành bài thi. Thí sinh hoàn thành bài thi cao thì có năng lực tốt hơn thí sinh hoàn thành bài thi thấp. Vấn đề của cách đánh giá này là khi thí sinh A và B có mức độ hoàn thành giống nhau, nhưng thí sinh A có thể giải quyết nhiều câu hỏi khó hơn thí sinh B, có thể nói thí sinh A có khả năng tốt hơn thí sinh B tuy nhiên với cách đánh giá truyền thống, hai thí sinh này có năng lực giống nhau. Tương tự như thế, khi đánh giá đề thi, độ khó của câu hỏi thường được dựa vào tỉ lệ học sinh trả lời sai. Nếu với 2 câu hỏi C và D có cùng tỷ lệ trả lời sai giống nhau, nhưng có nhiều học sinh khá giỏi trả lời sai câu hỏi C hơn câu hỏi D, thì rõ ràng câu hỏi C sẽ có mức độ khó cao hơn câu hỏi D, nhưng với phương pháp cũ lại không quan tâm đến những thông tin này. Lý thuyết IRT sử dụng cả năng lực học sinh và độ khó câu hỏi để đưa vào phân tích nhằm đưa ra những đánh giá tổng quát và chính xác hơn về khả năng của học sinh và mức độ của đề thi.
1. Lý thuyết IRT
IRT dựa trên mô hình toán học dùng để mô tả mối liên hệ giữa những đặc tính ẩn và những dấu hiệu có thể quan sát được. Ý tưởng về IRT được hình thành từ năm 1950 và được đẩy mạnh nghiên cứu ứng dụng vào những năm 1980. Lý thuyết IRT sử dụng 3 tham số chính để tính toán: độ khó của bài thi, mức độ phân loại học sinh của câu hỏi, mức độ phán đoán của thí sinh. Độ phán đoán dựa trên giả thiết là học sinh không biết câu trả lời đúng mà chỉ hoàn toàn dựa vào phán đoán để giải quyết câu hỏi.
Trong IRT lại phân ra 3 mô hình con [2]. Mô hình 1 biến, chỉ sử dụng tham số độ khó của bài thi để phân tích dữ liệu (còn được gọi là mô hình Rasch). Mô hình 2 biến, sử dụng tham số độ khó và độ phân loại. Mô hình 3 biến dùng cả 3 tham số để đánh giá dữ liệu. Càng nhiều tham số tham gia đánh giá thì độ phức tạp của mô hình càng tăng và mất nhiều thời gian hơn để phân tích và thu thập dữ liệu đầu vào. Trên thực tế, mô hình Rasch được sử dụng phổ biến nhất bởi sự cân bằng giữa các yếu tố của nó.
Công thức của mô hình Rasch [3]:

P: Xác suất trả lời đúng câu hỏi
theta: Năng lực của thí sinh
difficulty: độ khó của câu
Trong IRT có 3 biểu đồ chính cần phân tích: biểu đồ đặc tính câu hỏi, đường thông tin câu hỏi, sơ đồ so sánh thí sinh và câu hỏi.
Biểu đồ đặc tính câu hỏi
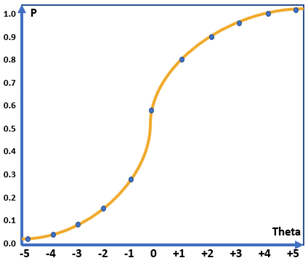
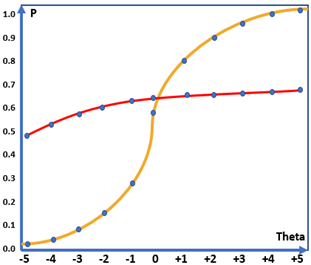
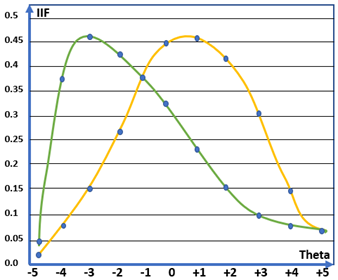
Trong lý thuyết IRT, đường đặc tính câu hỏi thể hiện xác suất trả lời đúng câu hỏi đối với từng năng lực học sinh. Như hình 1a, năng lực học sinh trải dài trong khoảng [-5;5], với năng lực là -4 thì xác suất trả lời đúng câu hỏi là 0.04, với năng lực +4, xác suất tăng lên đến 0.95. Đây có thể coi là đường đặc tính đặc thù có độ phân loại khá cao, chỉ những học sinh khá mới có xác suất trả lời đúng câu hỏi cao và ngược lại.
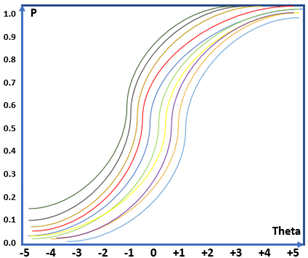
Đường đặc tính cho cả một bài thi gồm khoảng 10 câu sẽ tương tự như hình 1b.
(a) 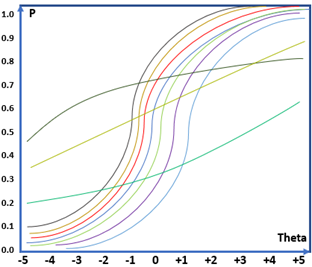
(b)
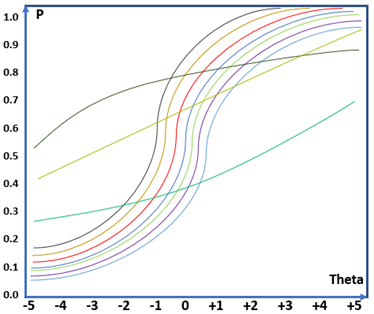
Nếu ta thêm tham số phân loại vào mô hình, đường đặc tính sẽ bắt đầu phức tạp hơn. Hình 2a thể hiện đặc tính của 2 câu hỏi, câu hỏi da cam có độ phân loại tốt đối với học sinh kém và khá giỏi. Tuy nhiên, câu hỏi màu đỏ có độ phân loại kém khi cả học sinh kém và khá đều có thể trả lời đúng với xác suất gần tương đương. Với một bài thi 40 câu thì đường đặc tính sẽ trông như hình 2b. Các đường đặc tính câu hỏi sẽ giao cắt lẫn nhau trông rất phức tạp. Để phân tích đường đặc tính câu hỏi có sự tương quan lẫn nhau trong cả 1 đề thi sẽ khá khó khăn.
Khi ta thêm tham số phán đoán vào mô hình, đường đặc tính sẽ gần tương tự như hình 2b, nhưng được nâng lên một bậc nhất định do có xác suất trả lời thành công do phán đoán. Để tính toán mức độ phán đoán cho từng người và từng câu hỏi sẽ rất phức tạp và mất thời gian.
Đường thông tin câu hỏi
Trong IRT, ngoài đường đặc tính cung cấp khái quát độ phân loại học sinh của câu hỏi, IRT còn đưa ra đánh giá độ hữu ích của câu hỏi trong từng giải năng lực thí sinh dựa vào đường thông tin câu hỏi (hình 4). Nếu trong đề thi có những câu hỏi quá khó, không một học sinh nào trả lời được, hoặc ngược lại, có những câu quá dễ, tất cả học sinh đều trả lời được thì đó là những câu hỏi không hữu ích và không cung cấp thông tin nào cả. Điều quan trọng nhất trong những cuộc thi hay kiểm tra là đánh giá năng lực và độ phân loại học sinh. Những câu hỏi vừa nêu trên không đưa ra được đánh giá phân loại học sinh, ta sẽ không thể biết học sinh nào tốt hơn/yếu hơn học sinh nào. Ta cũng có thể dễ dàng phán đoán được là độ thông tin hữu ích mà câu hỏi cung cấp sẽ càng thấp khi năng lực học sinh trải về 2 cực -5, +5. Hình 4 mô tả đường thông tin của 3 câu hỏi, câu hỏi màu vàng đưa ra nhiều thông tin nhất với dải năng lực từ -1 đến 3, trong khi đối với câu hỏi màu xanh là từ -4 đến -1.
Sơ đồ so sánh câu hỏi và thí sinh
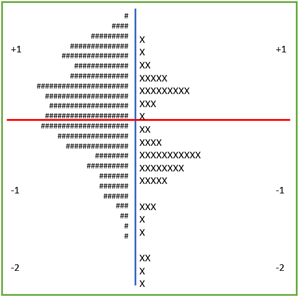
Sơ đồ câu hỏi và thí sinh đưa ra so sánh trực quan giữa độ khó của câu hỏi và năng lực thí sinh (hình bên trên). Bên trái sơ đồ là phổ năng lực học sinh, bên phải là phổ độ khó câu hỏi. Nếu kẻ một đường màu đỏ tại giá trị 0, có thể thấy rõ ràng là phần lớn thí sinh thể hiện khá tốt trong bài kiểm tra. Số học sinh ở góc trên bên trái đều trả lời đúng phần lớn câu hỏi của đề thi (góc dưới bên phải). Trong đó khoảng 8 câu hỏi dưới cùng bên phải có mức độ quá dễ, dễ hơn nhiều so với năng lực học sinh. Một đề thi được coi là phù hợp nếu độ khó của nó vừa khớp với năng lực thí sinh. Số câu hỏi nằm ngoài khoảng năng lực học sinh (trên và dưới) không nên quá nhiều.
Tính toán độ misfit
IRT đưa ra độ misfit để tính toán độ phù hợp và hữu ích của câu hỏi trong bài thi, hay chính xác hơn, là độ phù hợp của câu hỏi đối với loại mô hình IRT đang sử dụng. Một ví dụ hơi cường điệu là misfit sẽ phát hiện những câu hỏi vật lý trong một bài thi môn hóa. Thông thường, misfit đưa ra được những dấu hiệu bất thường của câu hỏi dựa vào thống kê và độ tương quan của năng lực học sinh với tỉ lệ chọn đáp án của câu hỏi. Những bất thường xảy ra đối với câu hỏi là đáp án bị sai, hay nội dung câu hỏi được thể hiện không rõ ràng gây ra sự hiểu nhầm cho thí sinh.
Để đo lường độ phù hợp của câu hỏi, ta sử dụng “chuẩn hóa Z” (ZSTD – Z Standardized). ZSTD đưa ra những thống kê xác suất của “độ lệch chuẩn hóa” (standardized residual) cho từng câu hỏi đối với mô hình. ZSTD có khi còn được coi là T-value trong một số bảng thống kê. Giá trị ZSTD có thể có giá trị âm khi kết quả thực tế quá khớp với giá trị kỳ vọng (overfitting).

Để đo lường độ hữu ích của câu hỏi, ta sử dụng “sai số bình phương trung bình” (MNSQ – Mean Square)
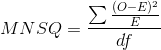
O – kết quả thực tế nhận được
E – kết quả kỳ vọng
df – bậc tự do (degree of freedom)

ZSTD và MNSQ lại phân ra thành 2 loại: outfit và infit. Outfit tính toán độ phù hợp trong đó không sử dụng hệ số đi kèm, trong khi infit có sử dụng hệ số đi kèm để giảm thiểu ảnh hưởng của những câu hỏi có độ lệch lớn so với các câu hỏi còn lại. Nếu infit = 1 nghĩa là câu hỏi hoàn toàn khớp với mô hình dùng để phân tích, nếu infit = 1.4 nghĩa là câu hỏi có khả năng lệch khỏi giá trị dự đoán khoảng 40%.
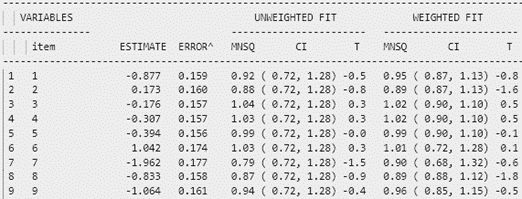
Hình 5 mô tả bảng tính toán misfit cho 9 câu hỏi. Cột “UNWEIGHTED FIT” tính giá trị outfit và cột “WEIGHTED FIT” tính giá trị infit của câu hỏi. Dưới cột “UNWEIGHTED FIT” và “WEIGHTED FIT” lại phân ra cột MNSQ và cột giá trị T (giá trị ZSTD). Thông thường ta sẽ hi vọng các giá trị MNSQ sẽ nằm trong trong khoảng tự tin (CI – Confidence Interval), nếu giá trị MNSQ (của cả infit và outfit) nằm ngoài khoảng tự tin chứng tỏ có bất thường xảy ra đối với câu hỏi đó. Với 9 câu hỏi trong hình 5, ta thấy tất cả các câu hỏi đều có giá trị MNSQ nằm trong khoảng tự tin, và giá trị T không bị đột biến.
2. Ứng dụng IRT vào phân tích dữ liệu
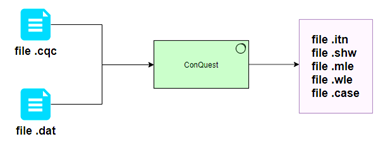
Phần mềm CONQUEST được sử dụng để ứng dụng lý thuyết IRT vào phân tích dữ liệu của đề thi và năng lực thí sinh. Đầu vào của phần mềm gồm 2 file. Một file cấu hình và một file dữ liệu. File cấu hình khai báo cấu trúc bài thi, dạng đáp án trắc nghiệm, yêu cầu phần mềm chạy mô hình IRT nào (Rasch, 2 biến, hay 3 biến) và yêu cầu thông đầu ra gồm các dữ liệu nào. File dữ liệu bao gồm các chuỗi câu trả lời của các thí sinh. Đầu ra của phần mềm phụ thuộc vào yêu cầu của file cấu hình, nhưng cơ bản sẽ có file đánh giá từng câu hỏi, sơ đồ so sánh năng lực học sinh và câu hỏi, bảng infit, outfit…
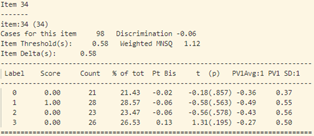
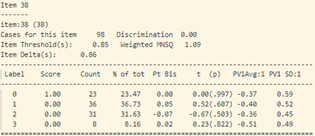
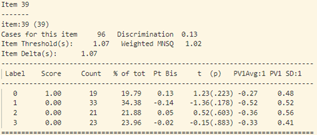
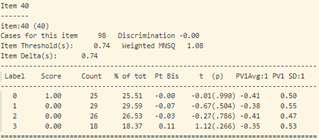
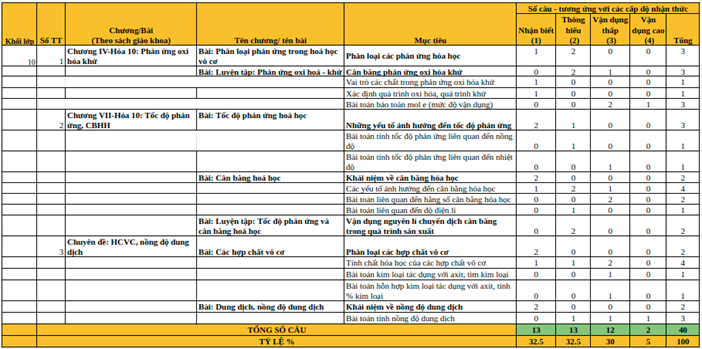
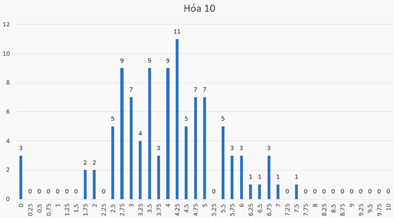
Ở đây ta có dữ liệu bài làm của 98 học sinh thi trắc nghiệm môn Hóa học kỳ 1 của một trường PTTH tại Hà Nội . Đề thi gồm có 40 câu, ma trận đề thi (chi tiết hình 7) gồm 13 câu nhận biết (từ câu 1 – 13), 13 câu thông hiểu (từ câu 14 – 26), 12 câu vận dụng (từ câu 27 – 38), và 2 câu vận dụng cao (câu 39, 40). Phổ điểm của thí sinh được thể hiện trong hình 8, có thể thấy rằng kết quả của thí sinh không được tốt, khoảng 80% thí sinh có điểm dưới trung bình. Cụ thể, 83 thí sinh dưới 5 điểm, 18 thí sinh trên 5 điểm. Tạm thời đánh giá rằng, đề thi môn hóa này khá khó so với phần lớn thí sinh.
Để phân tích kỹ hơn đề thi và năng lực học sinh, ta chạy phần mềm Conquest và ra kết quả như sau:
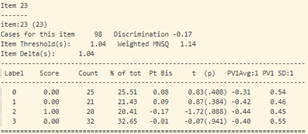
- Trong bảng tính toán misfit của 40 câu hỏi (như trong hình 15), cột “ESTIMATE” tính toán độ khó của từng câu hỏi. Cột “UNWEIGHTED FIT/OUTFIT” và cột “WEIGHTED FIT/INFIT” tính toán giá trị misfit của câu hỏi. Thông thường ta sẽ hi vọng các giá trị MNSQ sẽ nằm trong trong khoảng tự tin (CI – Confidence Interval), nếu giá trị MNSQ (của cả infit và outfit) nằm ngoài khoảng tự tin chứng tỏ có bất thường xảy ra đối với câu hỏi đó. Đối với bảng trong hình 15, câu hỏi 23 có giá trị outfit MNSQ = 1.34, trong khi khoảng CI: (0.72, 1.28). Dấu hiệu cho thấy rằng câu 23 có bất thường xảy ra và cần được giáo viên bộ môn xem xét lại. Khả năng lớn là câu hỏi có nội dung dễ gây hiểu nhầm hoặc đáp án của câu hỏi sai.

- Trong biểu đồ so sánh năng lực thí sinh – độ khó câu hỏi (chi tiết trong hình 16), ta thấy rằng câu hỏi 6, 18, 23, 32, 33, 38, 39 có độ khó vượt hẳn khỏi năng lực thí sinh, trong đó câu hỏi số 6 là câu hỏi nhận biết, câu 18, 23 là dạng thông hiểu, câu 32, 33, 38 là vận dụng, câu 39 là vận dụng cao. Tương tự, ở cận dưới của biểu đồ có câu 7, 10 thấp hơn nhiều so với trình độ thí sinh.
Tất nhiên, tùy theo yêu cầu của bộ môn chuyên ngành, đề thì cần có những câu dạng nhận biết rất cơ bản và hy vọng tất cả học sinh đều phải trả lời được, cũng như những câu rất khó có độ phân loại cao. Tuy nhiên, tất cả những những câu hỏi này có khả năng phân loại thí sinh thấp và đều cần được xét duyệt lại.

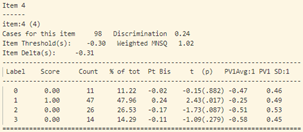
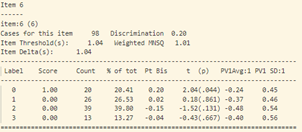
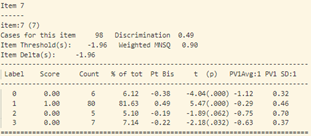
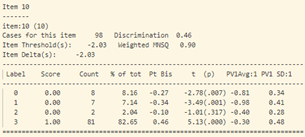
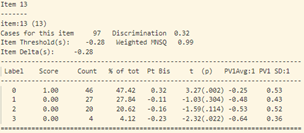
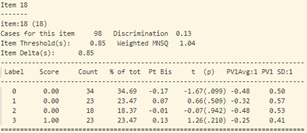
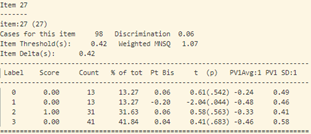
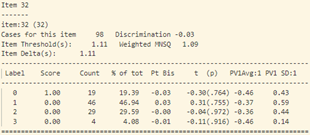
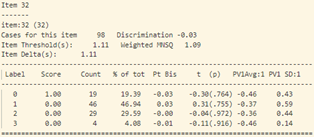
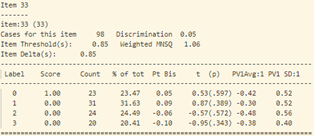
- Khi xem xét dữ liệu thống kê của từng câu hỏi (hình 17), sự bất thường được thể hiện chi tiết và rõ ràng hơn.
Trong những câu thuộc dạng nhận biết (từ câu 1 – 13), một số câu có tỷ lệ trả lời sai khá cao. Cụ thể như bảng thống kê sau:
| Câu hỏi | Tỷ lệ % |
| 2 | 63% |
| 3 | 55% |
| 6 | 80% |
- Tiếp tục phân tích độ phân loại và độ tương quan nhị phân của từng câu hỏi (hình 17) ta thấy:
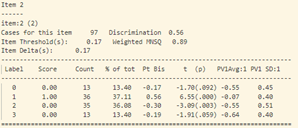
Tại câu 23 (câu hỏi dạng thông hiểu), độ phân loại thí sinh cực thấp: -0.17, phần lớn những học sinh trung bình lại có đáp án đúng (đáp án C) nhiều hơn (độ tương quan nhị phân Pt Bis: -0.17), trong khi những học sinh khá giỏi trong lớp thì lại chọn đáp án A, B (Pt Bis: 0.08 và 0.09).
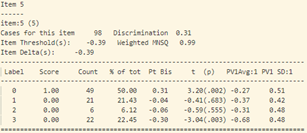
Tại câu 27 (câu hỏi dạng vận dụng) có đáp án đúng là C, thì lựa chọn C và A có độ phân loại khá tương đồng (Pt Bis: 0.06), trong đó năng lực trung bình của những thí sinh chọn đáp án A lớn hơn những thí sinh chọn đáp án C. Khả năng là nội dung câu 27 và lựa chọn A, C có độ gây hiểu nhầm lớn.
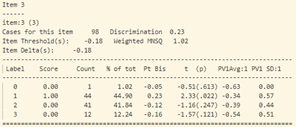
Tại câu 33 (câu hỏi dạng vận dụng), phần lớn thí sinh chọn đáp án B (đáp án sai), những học sinh này cũng có xu hướng khá giỏi hơn những học sinh chọn đáp án khác (Pt Bis: 0.09 và năng lực trung bình: -0.3)
Tương tự như vậy với câu 34, những học sinh khá lại chọn phương án D (đáp án sai). Độ phân loại của câu hỏi cũng cực thấp -0.06.

Với câu 38, những thí sinh khá có xu hướng chọn đáp án B, D (đáp án sai) với Pt Bis: 0.05 và 0.02
Bất thường cũng xảy ra với câu 40, phần lớn học sinh khá giỏi chọn D (đáp án sai) với Pt Bis: 0.11, năng lực trung bình cho nhóm thí sinh này cũng cao hơn các nhóm khác: -0.35. Độ phân loại của câu này cũng khá thấp: 0.00

- Tổng hợp lại, những câu hỏi cần được xem xét lại gồm: 2, 3, 6, 7, 10, 18, 23, 27, 32, 33, 34, 38, 39, 40.
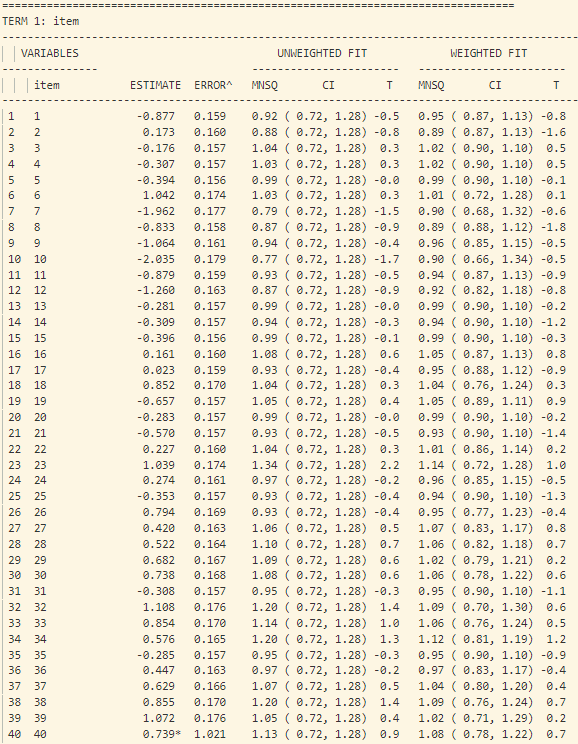
Hình 15 – Bảng Misfit cho từng câu hỏi 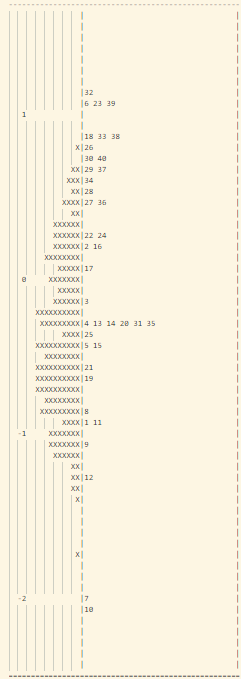
Hình 16 – Biểu đồ so sánh câu hỏi – thí sinh
Tham khảo
[1] Chen, Chih-Ming, Hahn-Ming Lee, and Ya-Hui Chen. “Personalized e-learning system using item response theory.” Computers & Education 44.3 (2005): 237-255.
[2] IRT tutorial. https://r.tquant.eu/KULeuven/IRT/. Accessed: 2020-01-30
[3] An, Xinming, and Yiu-Fai Yung. “Item response theory: What it is and how you can use the IRT procedure to apply it.” SAS Institute Inc. SAS364-2014 10.4 (2014).